Evolving Floorplans
Evolving Floor Plans is an experimental research project exploring speculative, optimized floor plan layouts. The rooms and expected flow of people are given to a genetic algorithm which attempts to optimize the layout to minimize walking time, the use of hallways, etc. The creative goal is to approach floor plan design solely from the perspective of optimization and without regard for convention, constructability, etc. The research goal is to see how a combination of explicit, implicit and emergent methods allow floor plans of high complexity to evolve. The floorplan is 'grown' from its genetic encoding using indirect methods such as graph contraction and emergent ones such as growing hallways using an ant-colony inspired algorithm.
The results were biological in appearance, intriguing in character and wildly irrational in practice. It was a fun learning experience and I plan to re-use methods in other projects.
Original layout
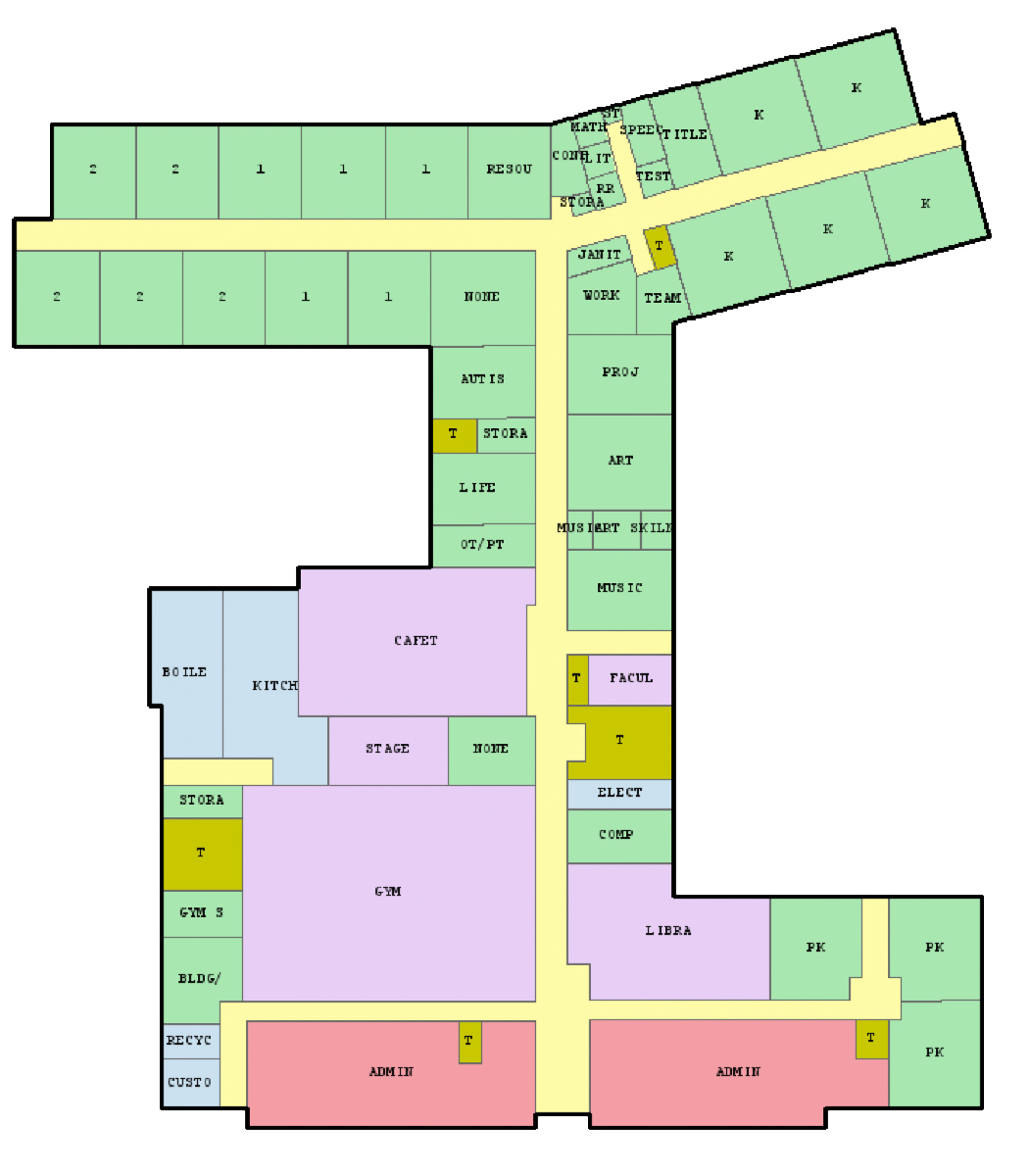
The original elementary school. Found somewhere in Maine.
'Optimized'
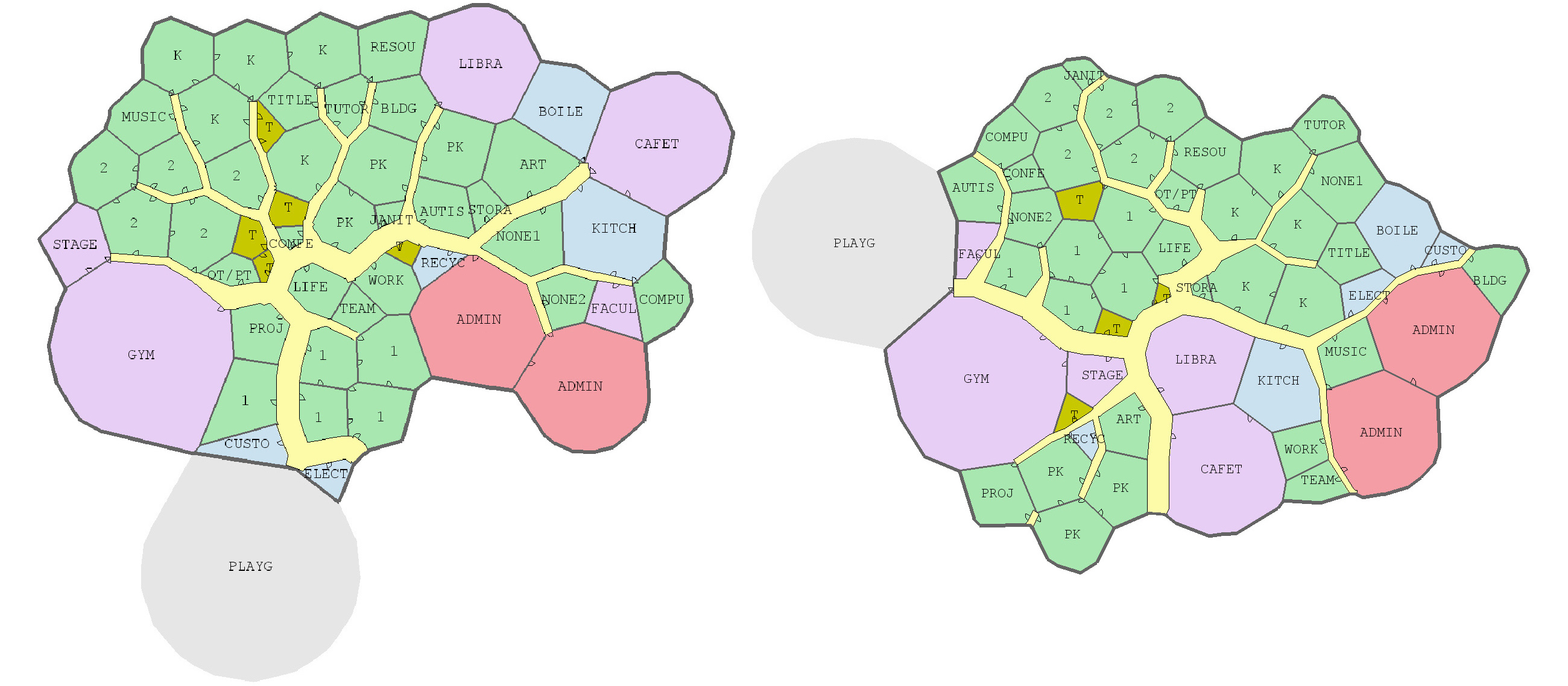
Left: Optimized for minimizing traffic flow bewteen classes and material usage. Right: Also optimized for minimizing fire escape paths.
Windows
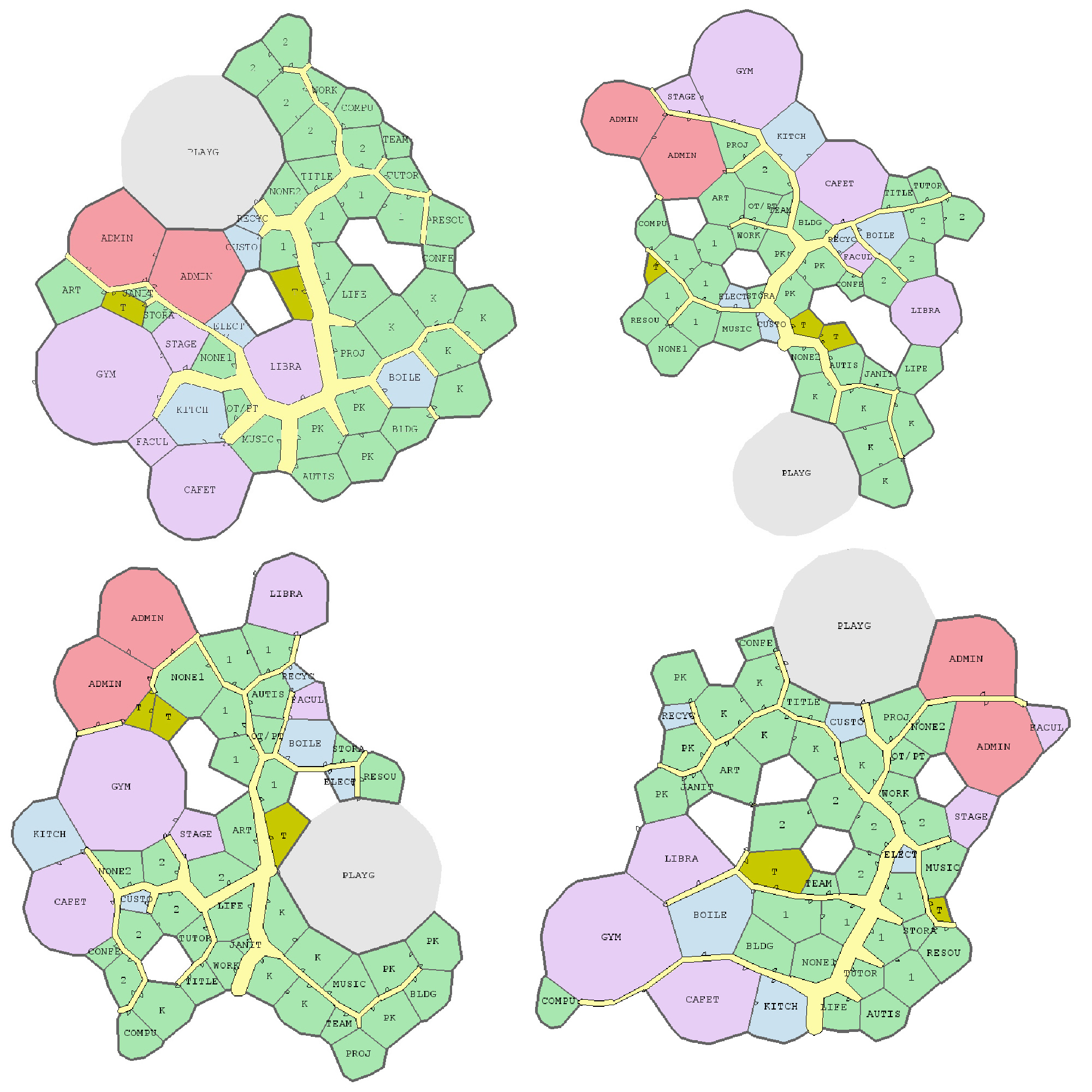
Windows were also experimented with as an additional fitness function. Classrooms had a higher priority than storage rooms. This led to many interior courtyards.
Background
A central challenge of spatial design problems is optimizing the relative positions, shapes and sizes of forms. Within architectural design, the layout of rooms is an early stage of the design process that is guided by multiple competing objective and subjective measures.
Recent computational tools that model the simulation of traffic, acoustics and heat conservation, among others, are allowing a more quantitative objective evaluation of forms. Converging with those abilities are advances in manufacturing, including CNC milling, on-site 3D printing, self-assembling structures and others, which are enabling new and more complex possible forms for which there are no simple means of designing. New tools for managing this complexity can empower designers to explore and optimize the increasingly high dimensional fitness spaces.
Methods
Two simulations, graph-contraction and ant-colony pathing, are used as 'growth processes'. Graph contraction is a family of algorithms that aim to create visually appealing layouts of a graphs. Ant-colony algorithms are probabilistic methods for finding optimal paths using a hive of emergent agents. Attribute genes encode meta-parameters that control various aspects of the simulations. This is analogous to developmental genes that establish patterns and guide development. Instead of encoding every path of all the hallways, a few attribute genes can optimize the entire layout.
The floor plan genome is a weighted, connected and undirected graph. Every desired room is represented with a node gene that contains information such as the room's size. Connection genes specify two node genes to span as well as a randomly initialized weight; they are added in a random manner until the graph is connected. Adjacency requirements create a subgraph with maximum edge weight. For example, the cafeteria must be adjacent to the kitchen. The genetic encoding is a generalization of NeuroEvolution of Augmenting Topologies (NEAT) that allows the artificial evolution of neural networks to graphs. This applies historical markers to allow crossover of graphs with varying topology. This allows floor plans to differ in the number of rooms they have.
Genotype To Phenotype Mapping
The mapping process from genome to phenotype is done in four parts. First, each node in the graph is arranged with a spectral layout to an intermediary position (figure 1a). Second, a physics simulation maps the intermediate positions to final coordinates that are the center of that room in the floor plan (figure 1b). Third, the room centers are converted into a polygonal mesh representing the walls (figure 1c, 1d). Fourth, the hallways are created along the edges of the mesh, and then pruned and finalized using an algorithm inspired by ant-colonies behavior and converted into a final geometry (figure 1e, 1f).
Mapping Overview
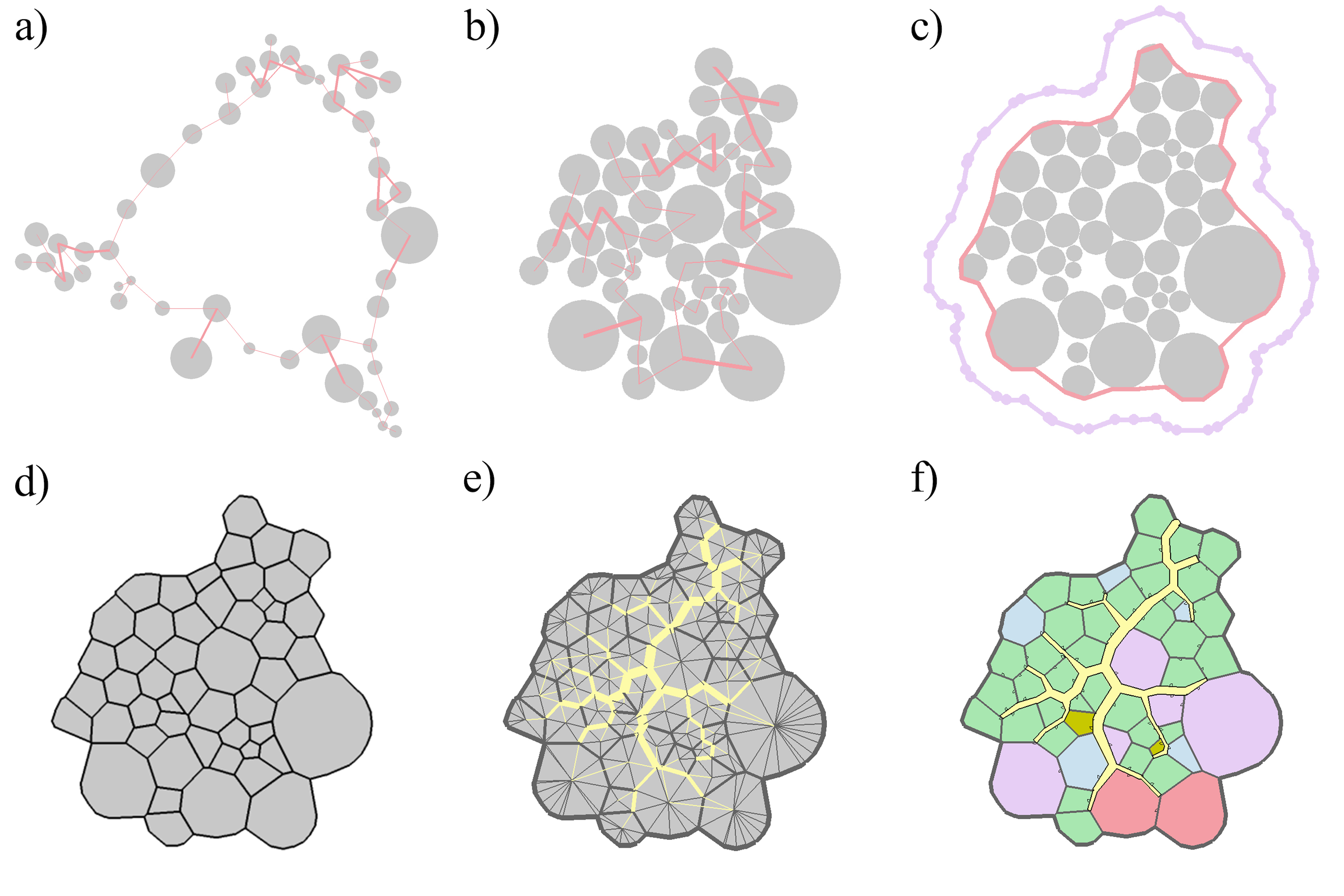
Figure 1: The complete mapping process. a) The initial physics simulation using a spectral layout as input. b) The final result of the physics simulation. c) The concave hull of points (red) has been inflated to produce boundary Voronoi seeds (purple circles). d) The Voronoi tessellation creates geometry mesh. e) The floor plan with interior edges added and results of the hallway algorithm drawn in yellow. f) The final floor plan phenotype. Hallways are merged into a final geometry and interior edges used for door placement.
Hallways
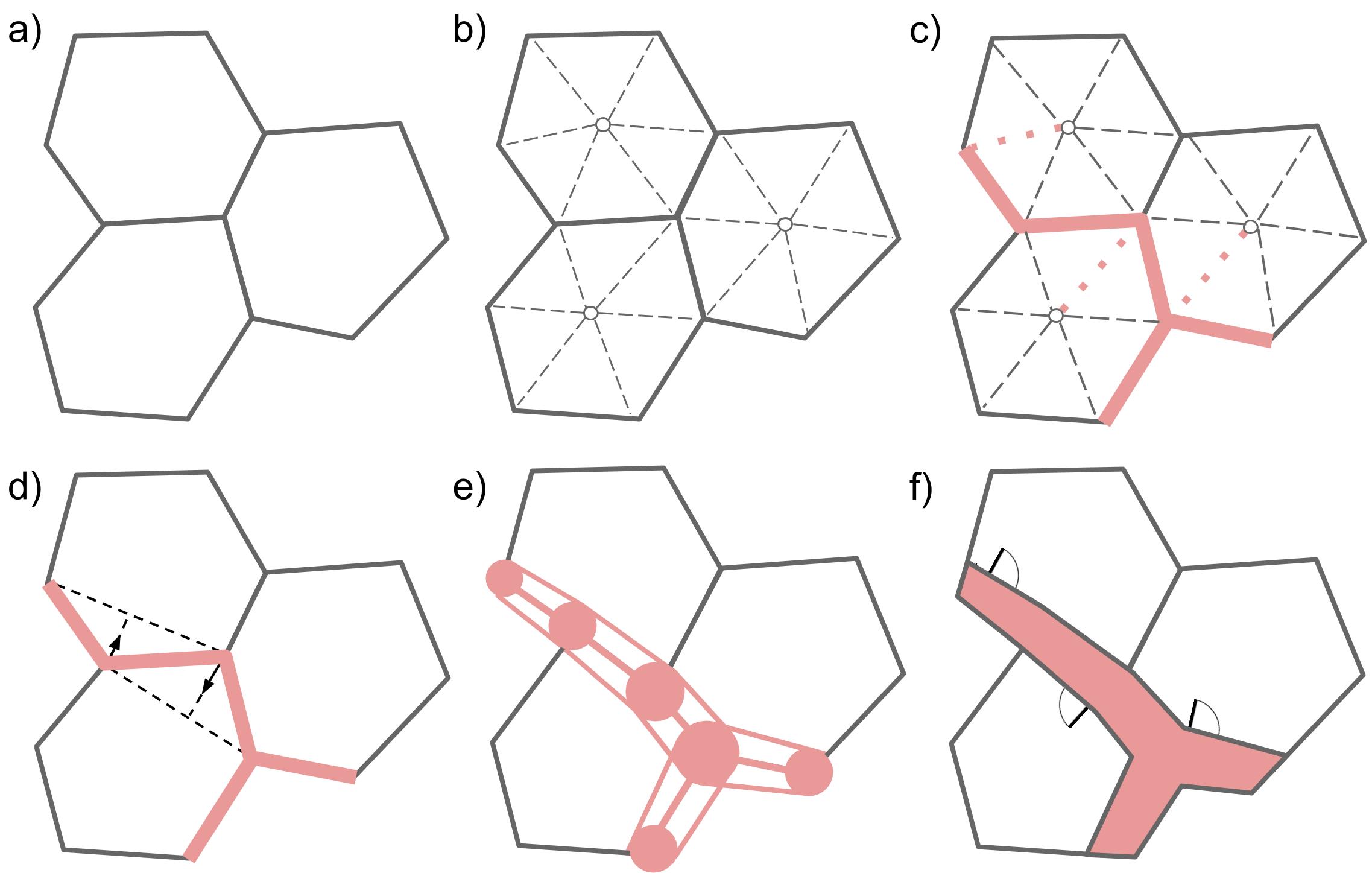
Figure 2: A representational overview of the hallway generation process. a) The mesh representation of a floor plan phenotype with three rooms. b) The creation of interior nodes and edges shown as hollow circles and dotted lines. c) The initial results of the OHP. Selected edges drawn in red. d) Smoothing of hallways by moving hallway vertices halfway to their projection onto the segment formed by neighbors. e) Creation of hallway geometry by using outer tangent lines of circles with radius proportional to travel load. f) The final hallway geometry with doors placed from interior edges with travel loads.
Future Work
A direction of work specific to schools is the mutual evolution of students' class schedules and floor plan layout. This would allow a unified optimization process of the entire school day experience. Genetic algorithms are already currently applied to optimal scheduling problems.
The metrics could be expanded to include terrain maps, sun paths, existing trees and other environmental input, allowing the buildings to be highly adaptive to their context. The physics simulation could force certain boundary shape constraints.
The method could be evaluated with other applications such as office layouts or hospitals. Hospitals could minimize critical routes such as between surgery and pathology labs or between nurses' rooms and patients. Office plans could aim to minimize acoustical problems, a common issue in open offices, or to minimize walking paths, while also maximizing the percentage of walking paths that are shared with employees from other departments.
Conclusion
I have very mixed feelings about this project. It was my first large generative design project, and I think the underlying ideas have a lot of potential. The work required for all the various steps is probably overly complicated. By not obeying any laws of architecture or design, it also made the results very hard to evaluate. I hope it elicits some ideas in the reader about the future of generativity and design.
References
- Michalek, J.J., Choudhary, R., Papalambros, P.Y.: Architectural layout design optimization. Eng. Optimization (2002)
- Merrell, Paul, Eric Schkufza, and Vladlen Koltun. "Computer generated residential building layouts." ACM Transactions on Graphics (TOG). Vol. 29. No. 6. ACM, 2010.
- Liu, Han, et al. "Constraint aware interior layout exploration for pre-cast concrete based buildings." The Visual Computer (2013)
- Nassar, Khaled. "New advances in the automated architectural space plan layout problem." Proceedings Computing in Civil and Building Engineering (2010).
- O'Reilly, UnaMay, and Martin Hemberg. "Integrating generative growth and evolutionary computation for form exploration." Genetic Programming and Evolvable Machines (2007)
- Bentley, P. J. & Kumar, S. (1999). Three Ways to Grow Designs: A Comparison of Embryogenies for an Evolutionary Design Problem. Genetic & Evolutionary Computation Conference.
- Hornby, Gregory S., and Jordan B. Pollack. "The advantages of generative grammatical encodings for physical design." Evolutionary Computation, 2001. Proceedings of the 2001 Congress on. Vol. 1. IEEE, 2001.
- Feng, Tian, et al. "Crowddriven midscale layout design." ACM Transactions on Graphics 35.4 (2016).
- Stanley, Kenneth O., and Risto Miikkulainen. "Evolving Neural Networks through Augmenting Topologies." Evolutionary Computation (2002).
- Weisstein, Eric W. "Graph Embedding." From MathWorld Wolfram Web Resource. http://mathworld.wolfram.com/GraphEmbedding.html
- Luo, Bin, Richard C. Wilson, and Edwin R. Hancock. "Spectral Embedding of Graphs." Pattern Recognition 36.10 (2003): 2213230. Print.
- Fruchterman, Thomas M. J., and Edward M. Reingold. "Graph Drawing by Forcedirected Placement." Software: Practice and Experience 21.11 (1991): 1129164. Print.
- Michalek, J.J., Choudhary, R., Papalambros, P.Y.: Architectural layout design optimization. Eng. Optimization (2002)
- Merrell, Paul, Eric Schkufza, and Vladlen Koltun. "Computer generated residential building layouts." ACM Transactions on Graphics (TOG). Vol. 29. No. 6. ACM, 2010.
- Liu, Han, et al. "Constraint aware interior layout exploration for pre-cast concrete based buildings." The Visual Computer (2013)
- Nassar, Khaled. "New advances in the automated architectural space plan layout problem." Proceedings Computing in Civil and Building Engineering (2010).
- O'Reilly, UnaMay, and Martin Hemberg. "Integrating generative growth and evolutionary computation for form exploration." Genetic Programming and Evolvable Machines (2007)
- Bentley, P. J. & Kumar, S. (1999). Three Ways to Grow Designs: A Comparison of Embryogenies for an Evolutionary Design Problem. Genetic & Evolutionary Computation Conference.
- Hornby, Gregory S., and Jordan B. Pollack. "The advantages of generative grammatical encodings for physical design." Evolutionary Computation, 2001. Proceedings of the 2001 Congress on. Vol. 1. IEEE, 2001.
- Feng, Tian, et al. "Crowddriven midscale layout design." ACM Transactions on Graphics 35.4 (2016).
- Stanley, Kenneth O., and Risto Miikkulainen. "Evolving Neural Networks through Augmenting Topologies." Evolutionary Computation (2002).
- Weisstein, Eric W. "Graph Embedding." From MathWorld Wolfram Web Resource. http://mathworld.wolfram.com/GraphEmbedding.html
- Luo, Bin, Richard C. Wilson, and Edwin R. Hancock. "Spectral Embedding of Graphs." Pattern Recognition 36.10 (2003): 2213230. Print.
- Fruchterman, Thomas M. J., and Edward M. Reingold. "Graph Drawing by Forcedirected Placement." Software: Practice and Experience 21.11 (1991): 1129164. Print.